今天第二篇,还是之前的经典论文(PNN)还是基于DNN的深度模型用于预测点击率,不过相比于FNN提出了不少新的idea,一起来看下吧。
原文:《Product-based Neural Networks for User Response Prediction》
1、原理
给大家举例一个直观的场景:比如现在有一个凤凰网站,网站上面有一个迪斯尼广告,那我们现在想知道用户进入这个网站之后会不会有兴趣点击这个广告,类似这种用户点击率预测在信息检索领域就是一个非常核心的问题。普遍的做法就是通过不同的域来描述这个事件然后预测用户的点击行为,而这个域可以有很多。那么什么样的用户会点击这个广告呢?我们可能猜想:目前在上海的年轻的用户可能会有需求,如果今天是周五,看到这个广告,可能会点击这个广告为周末做活动参考。那可能的特征会是:[Weekday=Friday, occupation=Student, City=Shanghai],当这些特征同时出现时,我们认为这个用户点击这个迪斯尼广告的概率会比较大。
传统的做法是应用One-Hot Binary的编码方式去处理这类数据,例如现在有三个域的数据X=[Weekday=Wednesday, Gender=Male, City=Shanghai],其中 Weekday有7个取值,我们就把它编译为7维的二进制向量,其中只有Wednesday是1,其他都是0,因为它只有一个特征值;Gender有两维,其中一维是1;如果有一万个城市的话,那City就有一万维,只有上海这个取值是1,其他是0。
那最终就会得到一个高维稀疏向量。但是这个数据集不能直接用神经网络训练:如果直接用One-Hot Binary进行编码,那输入特征至少有一百万,第一层至少需要500个节点,那么第一层我们就需要训练5亿个参数,那就需要20亿或是50亿的数据集,而要获得如此大的数据集基本上是很困难的事情。
回顾FM、FNN模型
因为上述原因需要将非常大的特征向量嵌入到低维向量空间中来减小模型复杂度,而FM(Factorisation machine)是很有效的embedding model:
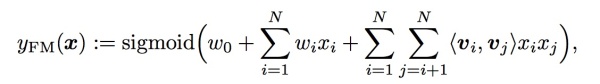
第一部分仍然为Logistic Regression,第二部分是通过两两向量之间的点积来判断特征向量之间和目标变量之间的关系。比如上述的迪斯尼广告,occupation=Student和City=Shanghai这两个向量之间的角度应该小于90,它们之间的点积应该大于0,说明和迪斯尼广告的点击率是正相关的。这种算法在推荐系统领域应用比较广泛。
那就基于这个模型来考虑神经网络模型,其实这个模型本质上就是一个三层网络:
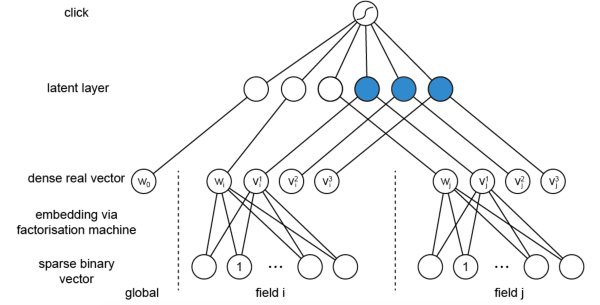
它在第二层对向量做了乘积处理(比如上图蓝色节点直接为两个向量乘积,其连接边上没有参数需要学习),每个field都只会被映射到一个low-dimensional vector,field和field之间没有相互影响,那么第一层就被大量降维,之后就可以在此基础上应用神经网络模型。
如用FM算法对底层field进行embeddding,在此基础上面建模就是FNN(Factorisation-machinesupported Neural Networks)模型:
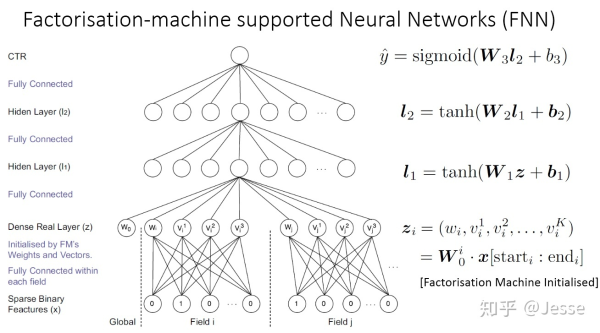
那现在进一步考虑FNN与一般的神经网络的区别是什么?大部分的神经网络模型对向量之间的处理都是采用加法操作,而FM 则是通过向量之间的乘法来衡量两者之间的关系。我们知道乘法关系其实相当于逻辑“且”的关系,拿上述例子来说,只有特征是学生而且在上海的人才有更大的概率去点击迪斯尼广告。但是加法仅相当于逻辑中“或”的关系,显然“且”比“或”更能严格区分目标变量。(加法就是正常拼接后作为输出,这里就是先做乘积再拼接(FM预训练得到嵌入向量)作为DNN的输入)
所以我们接下来的工作就是对乘法关系建模。可以对两个向量做内积和外积的乘法操作,在此基础之上我们搭建的神经网络PNN:提出了一种product layer的思想,即基于乘法的运算来体现特征交叉的DNN网络结构,如下图:
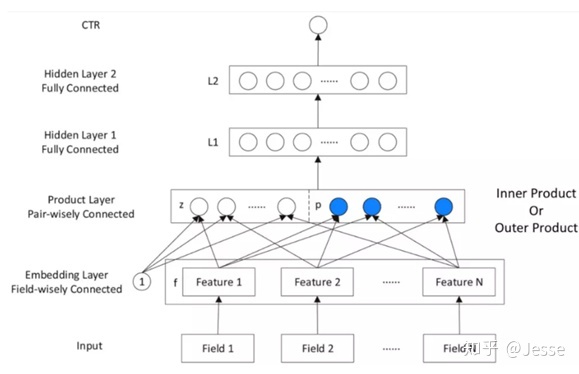
按照论文的思路,从上往下来看这个网络结构:
输出层 输出层很简单,将上一层的网络输出通过一个全连接层,经过sigmoid函数转换后映射到(0,1)的区间中,得到我们的点击率的预测值:
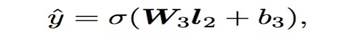
l2层
根据l1层的输出,经一个全链接层 ,并使用relu进行激活,得到我们l2的输出结果:

l1层
l1层的输出由如下的公式计算:
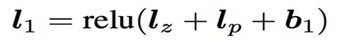
可以看到在得到l1层输出时,这里输入了三部分,分别是lz,lp 和 b1,b1是偏置项,这里可以先不管。lz和lp的计算就是PNN的重点所在了。
Product Layer
product思想来源于,在ctr预估中,认为特征之间的关系更多是一种and“且”的关系,而非add”或”的关系。例如,性别为男且喜欢游戏的人群,比起性别男和喜欢游戏的人群,前者的组合比后者更能体现特征交叉的意义。
product layer可以分成两个部分,一部分是线性部分lz,一部分是非线性部分lp。二者的形式如下:
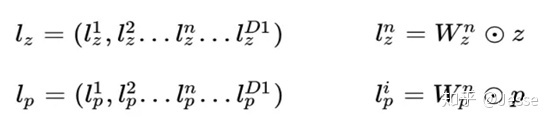
在这里,我们要使用到论文中所定义的一种运算方式,其实就是矩阵的点乘(对应位置相乘然后求和,最终得到的是一个标量):
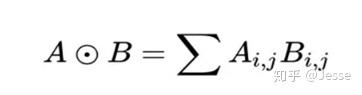
这里先继续介绍网络结构,下一章中详细介绍Product Layer。
Embedding Layer
Embedding Layer跟DeepFM中相同,将每一个field的特征转换成同样长度为D的向量,这里用f来表示。
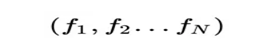
损失函数
损失函数使用交叉熵:
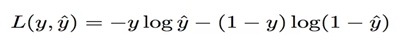
2、Product Layer详细介绍
前面提到了,product layer可以分成两个部分,一部分是线性部分lz,一部分是非线性部分lp。它们同维度,其具体形式如下:
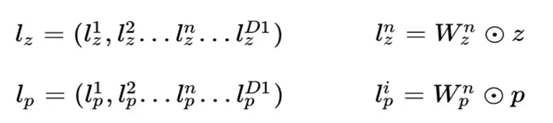
其中z,p为信号向量,z为线性信号向量,p为二次信号向量,$W_{z}^{i},W_{p}^{i}$为权重矩阵(权重矩阵与z,p同维,经过定义的这种点乘运算后都得到一个标量作为DNN的输入)。
看上面的公式,我们首先需要知道z和p,这都是由我们的embedding层得到的,其中z是线性信号向量,因此我们直接用embedding层得到:
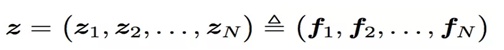
论文中使用的等号加一个三角形,其实就是相等的意思,可以认为z就是embedding层的复制。
对于p来说,这里需要一个公式进行映射:
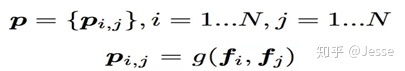
不同的g函数的选择使得我们有了两种PNN的计算方法,一种叫做Inner PNN,简称IPNN,一种叫做Outer PNN,简称OPNN。
接下来分别来具体介绍这两种形式的PNN模型,由于涉及到复杂度的分析,所以我们这里先定义Embedding的大小为M,field的大小为N,而lz和lp的长度为D1。
2.1 IPNN
IPNN中p的计算方式如下,即使用内积来代表pij:
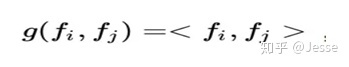
所以,pij其实是一个数(标量),得到一个pij的时间复杂度为M,p的大小为N×N,因此计算得到p的时间复杂度为N×N×M。而再由p得到lp的时间复杂度是N×N×D1。因此 对于IPNN来说,总的时间复杂度为N×N(D1+M)。文章对这一结构进行了优化,可以看到,我们的p是一个对称矩阵,因此我们的权重也是一个对称矩阵,对这个对称矩阵进行如下的分解:
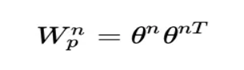
因此:
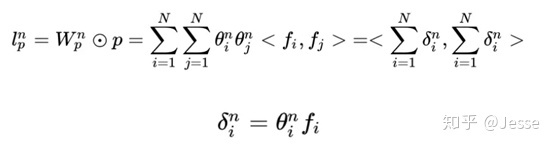
因此:

2.2 OPNN
OPNN中p的计算方式如下:
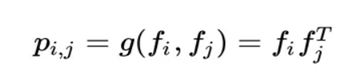
此时pij为M×M的矩阵,计算一个pij的时间复杂度为M×M,而p是N×N×M×M的矩阵,因此计算p的事件复杂度为N×N×M×M。从而计算lp的时间复杂度变为D1×N×N×M×M。这个显然代价很高的。为了减少复杂度,论文使用了叠加的思想,它重新定义了p矩阵:
通过元素相乘的叠加,也就是先叠加N个field的Embedding向量,然后做乘法,可以大幅减少时间复杂度,定义p为:
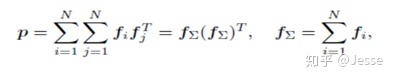
这里计算p的时间复杂度就变为了D1×M×(M+N)。
3、Discussion
和FNN相比,PNN多了一个product层,和FM相比,PNN多了隐层,并且输出不是简单的叠加;
在训练部分,可以单独训练FNN或者FM部分作为初始化,然后BP算法应用整个网络,那么至少效果不会差于FNN和FM;
4、Experiments
使用Criteo和iPinYou的数据集,并用SGD算法比较了7种模型:LR、FM、FNN、CCPM、IPNN、OPNN、PNN(拼接内积和外积层),正则化部分(L2和Dropout);
实验结果如下图所示:
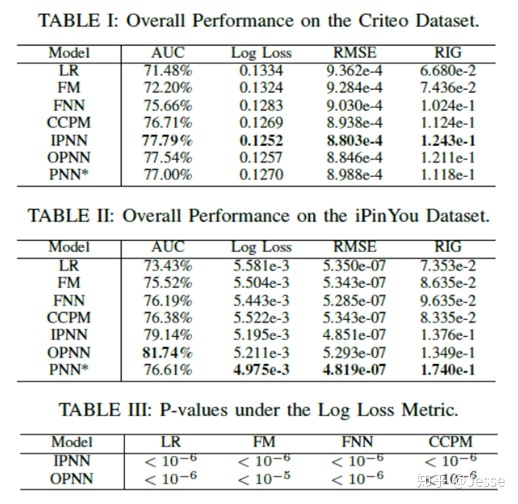
结果表明PNN提升还是蛮大的;这里介绍一下关于激活函数的选择问题,作者进行了对比如下:
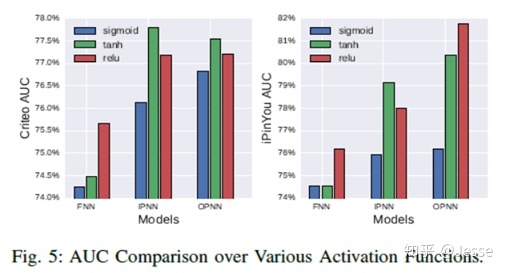
从图中看出,anh在某些方面要优于relu,但作者采用的是relu,relu的作用: 1、稀疏的激活函数(负数会被丢失);2、有效的梯度传播(缓解梯度消失和梯度爆炸);3、有效的计算(仅有加法、乘法、比较操作)。
实现PNN的一个Demo,感兴趣的童鞋可以看下我的github。